Suggesting email address using string similarity algorithm
Recently, we noticed a large number of unconfirmed accounts. Those were not spam accounts they looked like legit users. Are we losing customers that early in the funnel? When we looked closely we noticed a similar pattern:
[email protected]
[email protected]
[email protected]
[email protected]
All of those email addresses have a mistyped domain. That’s not great. I could imagine a customer refreshing their inbox, waiting for a confirmation email, and cursing the internet.
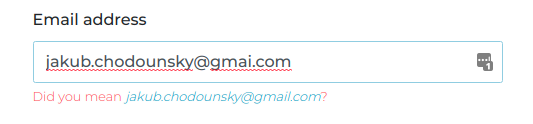
What could we do to improve the onboarding experience? What if we could detect typos and suggest a correct email for them?
Did you mean [email protected]?
That would be really cool. And luckily for us there is a few neat algorithms that can help us with that.
In computer science this is an exercise of approximate string matching. And we will use a string distance (or sometimes called a string metric) to quantify how close two words – email domains in our case – are to each other.
Levensthein Distance
The most common string metric is Levenshtein distance (also called edit distance). It tells you the minimum number of edits – insertion, deletion, substitution – that need to take place to get to the same word.
For example gnail.com and gmail.com would have Levensthein distance of 1. You need to substitute one character to get to the same word. Those two strings are very similar.
We can normalise the distance between 0.0 and 1.0 where 0.0 is not similar at all and 1.0 is an exact match. That’s a good idea to do for different string lengths. For that, we divide the edit distance by the length of the longest string and subtract that from 1. For our example it would end up to be 0.88.
Levensthein distance is usually implemented with dynamic programming using a variation of Wagner-Fischer algorithm. Below is a Javascript version from Andrei Mackenzie.
var getEditDistance = function(a, b){
if(a.length == 0) return b.length;
if(b.length == 0) return a.length;
var matrix = [];
var i;
for(i = 0; i <= b.length; i++){
matrix[i] = [i];
}
var j;
for(j = 0; j <= a.length; j++){
matrix[0][j] = j;
}
for(i = 1; i <= b.length; i++){
for(j = 1; j <= a.length; j++){
if(b.charAt(i-1) == a.charAt(j-1)){
matrix[i][j] = matrix[i-1][j-1];
} else {
matrix[i][j] = Math.min(matrix[i-1][j-1] + 1,
Math.min(matrix[i][j-1] + 1,
matrix[i-1][j] + 1));
}
}
}
return matrix[b.length][a.length];
};
Trigram
Levensthein distance is a nifty algorithm but we found it didn’t work particularly well for our dataset. Also, it not easy to scale but for this use case it doesn’t matter.
There is a few other alternatives. We decided to go for Jaccard distance over Trigram vectors. It sounds scary but don’t be afraid.
Trigrams are three consecutive letter groups from a string. They are often used in natural language processing as they are relatively cheap to make and provide you with additional context of neighbouring characters.
Firstly, we decompose a string into trigrams.
trigram('hello');
[' h', ' he', 'hel', 'ell', 'llo', 'lo ']
And the code for the above.
var trigram = function(string) {
const padded = ` ${string} `.toLowerCase();
let gramStart = 0;
let gramEnd = 3;
const grams = [];
while (gramEnd <= padded.length) {
grams.push(padded.substring(gramStart, gramEnd));
gramStart += 1;
gramEnd += 1;
}
return grams;
}
After that, we can calculate the distance. It is a ratio of matching trigrams to their union.
var distance = function(aGrams, bGrams) {
const matches = aGrams.filter(value => bGrams.includes(value));
const uniqueGrams = [...new Set(aGrams.concat(bGrams))];
return Number((matches.length / uniqueGrams.length).toFixed(2));
}
var compare = function(a, b) {
const aGrams = trigram(a);
const bGrams = trigram(b);
return distance(aGrams, bGrams);
}
With the final number we need to decide what threshold is a possible match. I’d like to say that we did an extensive testing on our dataset to get the perfect distance but we haven’t.
Instead, we looked at Postgres pg_trgm extension and used their default of 0.3. And it worked out great.
Conclusion
Last step is hooking these functions up to our registration form. We extract the domain from the input, lowercase it, and remove any white space.
Then, we run it against a dictionary of our confirmed email domains that have at least a few users registered. That covers most of our basis and runs pretty quickly on a client.
And with that, we save a customer or two from abandoning the registration.
Resources
- Understanding Levensthein Distance for Beginners
- js-levensthein
- N-gram similarity and distance
- Similarity in Postgres and Rails using Trigrams
- pg_trgm
- Super fast string matching in Python
- String Similarity Algorithms Compared
- A Comparison of String Distance Metrics for Name-Matching Tasks
- Comparison of String Distance Algorithms